Be careful of the orbit chosen for a low-orbiting lunar satellite. 'What counts is an orbit's inclination,' that is, the tilt of its plane to the Moon's equatorial plane. 'There are actually a number of 'frozen orbits' where a spacecraft can stay in a low lunar orbit indefinitely. About Frozen Orbit: “. Hard science fiction and an entertaining and gripping plot. Chiles nails the atmosphere of a NASA-run human spaceflight mission in the 21st century, the.

Frozen orbits about the Earth – counteracting orbital perturbations in the long run

A special type of orbit that is cleverly chosen such that the variation in the mean Kepler elements under the influence of Earth’s irregular gravity field is minimized.

There are six intuitive orbital components that are often used to describe the shape and orientation of a satellite orbit. These elements are varying constantly due to perturbations, but for a cleverly chosen orbit, the frozen orbit, the long-term effects of at least some of these perturbations can be cancelled.

In 1978, a key Earth observation satellite was launched from Vandenberg AFB in the United States. This satellite, carrying the name Seasat, was to monitor Earth’s oceanographic phenomena. To carry out this mission, the satellite was equipped with an array of Earth observation instruments, such as the first space-borne Synthetic Aperture Radar (SAR) and a radar altimeter. To maximize the quality of the data from these instruments, the orbit had to be carefully selected in order to minimize the influence of orbital perturbations. As such, Seasat was the first mission to make use of a so-called ‘frozen orbit’.

1. So you can finally earn a good legendary sniper by just playing pvp. But is it any good?Social Media:Follow me on Twitch: https://www.twitch.tv/ZkMushroomFo.
2. Patrick Chiles suggests that in 1991 the USSR improbably sent a ship to Pluto using atomic bombs for thrust. For some reason the cosmonauts stayed in Frozen Orbit (Trade from Baen).
3. In orbital mechanics, a frozen orbit is an orbit for an artificial satellite in which natural drifting due to the central body 's shape has been minimized by careful selection of the orbital parameters. Typically, this is an orbit in which, over a long period of time, the satellite's altitude remains constant at the same point in each orbit.

The paper on the orbit design of Seasat, (Cutting et al, 1978) demonstrated the existence of a family of near-circular polar orbits that suffered from minimal secular variations in the mean argument of pericenter (ω) and the mean eccentricity (e). Normally, these two orbital elements suffer from variations caused by the flattening of the Earth at the poles (the equatorial bulge, or J₂-effect). It is possible to ensure static behavior of the argument of pericenter and the eccentricity by placing the satellite in an orbit at the critical inclination (63.4 degrees), but global coverage is not possible at this inclination. For Seasat, a minimal variation in both the mean argument of pericenter and mean eccentricity was a necessity, as this would guarantee a constant altitude profile above Earth’s surface as a function of latitude only. Theoretically, this would eliminate the need for corrective maneuvers.

Despite Seasat’s early failure after just 105 days in orbit, it gathered more oceanographic altimetry data than all other surface-based efforts before it. The newly applied frozen orbit concept proved to be successful and has been applied to numerous missions since. Well-known Earth observation missions such as Envisat, ERS-1 and ERS-2 all fly in Sun-synchronous, repeating ground track frozen orbits.

The analytical way

One of the pillars of orbital perturbation theory is a set of six equations governing the rate of change of all six orbital elements – the so-called Lagrange equations. These equations are expressed in terms of disturbing potential, which is a location-dependent correction of the simple spherical symmetric point-mass gravitational potential. Kingdom come deliverance console commands carry weight. The disturbing potential is often formulated in terms latitude-dependent (zonal) terms, longitude-dependent (sectorial) terms, and terms depending on both latitude and longitude (tesseral). If only the first two zonal terms of the gravity field expansion (the J₂-effect and the J₃-effect) are taken into account, it is possible to derive a simple set of conditions linking the mean eccentricity and mean argument of pericenter together:

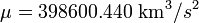
Where e, a, i and ω denote the mean eccentricity, semi-major axis, inclination and argument of pericenter, respectively. R_E is Earth’s equatorial radius, and J₂ and J₃ are the coefficients for the zonal expansion of the gravity field. Simple as the equation for the frozen eccentricity may be, its derivation is rather complicated. Additionally, it is emphasized that only taking into account the first two zonal terms of the gravity field does not make for a very realistic representation. However, the complicated derivation can be repeated for more realistic zonal gravity field models, and though the resulting expressions are nowhere near elegant, they can be solved numerically. This way, it can be shown that the inclusion of higher degree zonal terms (all the way up to J₂₅, for example) has a significant effect on the final frozen eccentricity. Many more research efforts have been put into further refining the required conditions for a frozen orbit, most of them venturing deep into the field of higher order astrodynamics. However, most of these methods rely on formulating the perturbing accelerations as a disturbing potential, and this limitation may be overcome when using a purely numerical method to find frozen orbit conditions.

Mean vs. osculating elements

The prediction of a satellite trajectory is made easy nowadays by numerically integrating the equation of motion, to which models for various orbital perturbations can be added. Aerodynamic drag, solar radiation pressure, third-body gravity and of course, Earth’s irregular gravity field; all of these can be taken into account. However, numerically integrated orbits result in state predictions in terms of osculating orbital elements, whose behavior is governed by short-periodic, long-periodic, secular and continuous variations, caused by orbital perturbations. It is possible to remove these effects and thus to transform from osculating to mean elements by making use of the so-called Eckstein-Ustinov theory (Spiridonova et al, 2014) and numerical averaging. Especially for near-circular orbits it is not possible to transform from osculating to mean elements by averaging only.

With such a tool, it is possible to take a closer look at the behavior of the mean eccentricity and mean argument of pericenter for a satellite actually flying in a frozen orbit. In Figure 1, the evolution of these elements has been plotted for ERS-2 throughout 2004, showing nearly static behavior close to the original design values. This serves as verification for reconstruction methods.

Figure 1 – Evolution of the actual mean argument of pericenter and mean eccentricity of ERS-2 in 2003. Green and red marks the start and end of the year, respectively, and each dot marks the averaged mean orbital elements for a day.

Frozen Orbit Farm

Optimization to find frozen conditions

With the mean elements available, and with the goal to minimize variations in two of these components, it is possible to approach this goal as an optimization problem. This can be done by numerically integrating the trajectories resulting from a variety of injection positions and velocities, and evaluating the variations in the mean argument of pericenter and the mean eccentricity for these predicted trajectories. The resulting approach can be verified for the case of using simple zonal gravity field models, as for these models the numerical method can be compared to analytical solutions. The found frozen mean eccentricities match to within 0.1%.

When looking for the frozen eccentricity in realistic force models, e.g. taking into account drag, radiation pressure, third-body gravity and a gravity field model complete up to degree and order 25, it follows that the frozen conditions do not significantly change when compared to the case of a simple zonal model complete up to degree 10 (J₁₀). Therefore, the analytical solution ‘does the job’ just as well.

The influence of non-zonal perturbations can be determined by numerically integrating the found frozen orbit by including various perturbations, as shown in Figure 2. From this figure, it becomes apparent that radiation pressure is the most influential perturbation, next to the inclusion of tesseral and sectorial gravity field terms. ERS-2 is not affected by radiation pressure as much (Figure 1), as it is placed in a Sun-synchronous orbit.

Figure 2 – Evolution of the simulated mean argument of pericenter and mean eccentricity for a frozen orbit under the influence of several non-zonal perturbations. Time between marks is one week.

Looking back & looking ahead

The combination of numerical integration, optimization, and transformation from osculating to mean elements has led to an alternative design method for frozen orbits. Whilst being quite computationally expensive and performing just as well as simpler analytical models, there is potential in the chosen approach. The objective function used to minimize variations in the mean argument of pericenter and mean eccentricity can be adapted to minimize variations in other orbital elements, or optimize for a certain variation (a Sun-synchronous orbit, for example).

Frozen Orbit How To Get

Let’s take a look at the PVE God Roll for Frozen Orbit, a void energy sniper rifle released during Season of the Chosen. The Frozen Orbit is a 72 RPM aggressive frame sniper rifle with high damage at the cost of high recoil. This weapon is great for bosses that have damage phases. This weapon would be difficult to use in boss fights like the new Proving Ground strike because the Boss moves and jumps around the map. My issue with this weapon is the amount of perk combination Frozen Orbit can roll with. It will make you pull your hair out because it’s near impossible to get the roll you want unless you are grinding daily in the Crucible. Oh, and did I mention you can only get it in the Crucible? Here is the PVE God Roll for Frozen Orbit.

Corkscrew Rifling is a balanced barrel. It increases stability by 5 for a total of 39. Increases the range by 4, for a total of 79, and increases handling by 4 for a total of 32.

Appended Mag. This weapon’s magazine is built for higher capacity. It increases the size by 1 for a total of 4.

Tap The Trigger grants a short period of increased stability and accuracy on the initial trigger pull.

Vorpal Weapon. Increased damage against bosses, vehicles, and Guardians with their Super active. The increased damage is about 15% to Bosses and 50% damage to Guardians in their Super.

Reload masterwork increases the range by 9 for a total of 46. Boss Spec for a 7% increase in damage to bosses.

God Roll Frozen Orbit Destiny 2

Now you know the roll for Frozen Orbit for PVE. You can get this weapon completing crucible matches. If you want to increases your drop. Masterwork a Ghost and insert Prosperity (Crucible) to increases the chances of earning additional legendary gear. Get to grinding Guardian.

dimwishlist:item=3473290087&perks=4090651448,1087426260,3400784728,1546637391,758092021